Those wishing a historical perspective are free to read on!
For read-mostly data structures, performance can be greatly improved by using asymmetric locking primitives that provide reduced overhead for read-side accesses in exchange for more expensive write-side accesses. One example of such a primitive is the distributed reader-writer spinlock, which allows read-side lock acquisition to take place with no expensive references to globally shared state in the common case [11].
This paper takes asymmetric locking to its logical extreme, permitting read-side access with no locking or synchronization operations whatsoever. Of course, this means that updates do not block reads, so that a read-side access that completes shortly after an update could return old data. However, any reading thread that starts its access after an update completes is guaranteed to see the new data. This guarantee is sufficient in many cases. In addition, data structures that track state of components external to the computer system (e.g., network connectivity or positions and velocities of physical objects) must tolerate old data because of communication delays. In other cases, old data may be flagged so that the reading threads may detect it and take explicit steps to obtain up-to-date data, if required [10, 15].
Section 3 introduces concepts underlying read-copy update. Section 4 presents an implementation of read-copy update. Section 5 compares measured read-copy update performance to that of a simple spinlock. Section 6 analytically compares read-copy update to other locking primitives. Section 7 discusses related work, and Section 8 presents summary and conclusions.
Section 3.1 gives a brief intuitive introduction to read-copy update. Section 3.2 gives rigorous definitions of several important terms. Section 3.3 expands on these definitions with examples. Section 3.4 presents examples of how read-copy update might be applied to a number of different programming environments. Section 3.5 describes several different read-copy update architectures.
Data structures in a parallel environment generally cannot be assumed to be stable unless the corresponding update disciplines are followed, for example that particular locks are held. Once these locks are released, no prior-knowledge assumptions can be made about the state of any data structures protected by those locks. Therefore, if a given thread currently holds no locks, it cannot make any prior-knowledge assumptions about any data structure that is protected by any lock. A thread that is holding no locks is said to be in a quiescent state with respect to any lock-protected data structure. Such a thread cannot actively reference or modify any data structure guarded by a lock.
The keystone of read-copy update is the ability to determine when all threads have passed through a quiescent state since a particular point in time. This information is valuable—if all threads have passed through a quiescent state during a particular time interval, they are all guaranteed to see the effects of any change made prior to the start of that interval. This guarantee allows many algorithms to be constructed using fewer locks, and, in some specialized but commonly occurring cases, using no locks whatsoever. Reducing the number of locks simplifies deadlock avoidance, reduces lock and memory contention, and decreases synchronization overhead, all of which in turn result in simpler and faster programs.
Guarded data structure: A data structure that cannot safely be accessed and/or updated without possessing the proper token, lock, or identity.
Quiescent state: A state beyond which a thread makes no assumptions based on prior knowledge of any guarded data structures. Although it is possible to consider quiescent states with respect to particular data structures, this paper will use "quiescent state" in the universal sense unless otherwise stated.
Quiescent period: A time interval during which each thread passes through at least one quiescent state. Note that any time interval that encloses a quiescent period is itself a quiescent period.
Summary of thread activity: A set of data structures that are used to identify quiescent periods.
3.3 QUIESCENT STATES AND PERIODS
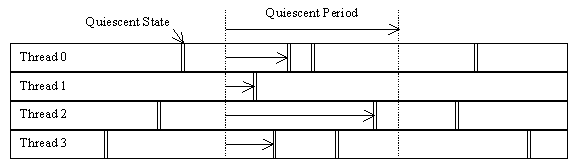
Figure 1 shows the relationship between quiescent states and quiescent periods. Each row in the figure represents the sequence of states that the corresponding thread passes through, with time progressing from left to right. The double vertical bars represent quiescent states.

Figure 1: QUIESCENT STATES AND PERIODS
The area between the pair of dotted vertical lines is a quiescent period, since each thread passes through at least one quiescent state during this time. The horizontal arrows show the maximum length of time that each thread can legitimately make assumptions based on prior knowledge of state preceding the start of the quiescent period. Any prior knowledge of the state of any guarded data structure held by any of the threads at the beginning of the quiescent period must be forgotten by the end of that quiescent period.
This property of quiescent periods guarantees that any change made before the beginning of a quiescent period will be observed by all threads by the end of that quiescent period. This guarantee can be used to construct extremely low-overhead update disciplines. Furthermore, since locks are not needed on the read side, deadlock issues are in some cases avoided. The following two sections show example update disciplines based on quiescent periods.
3.3.1 LOCK-FREE LINKED-LIST ACCESS
If a thread removes all references to a given data structure, it may safely free up the memory comprising that data structure after the end of the next quiescent period. Note that threads traversing the data structure need not acquire any locks. The required synchronization is achieved implicitly through the quiescent states—the quiescent period guarantees that no threads reference the data structure. Eliminating read-side locking can greatly increase speedups in the many cases where updates are rare. This same effect can be achieved using a garbage collector (in environments possessing them), but at greater cost. This greater cost stems from the need to modify otherwise-read-only data to indicate that a reference is held.
For a concrete example, consider a singly linked list with Thread 0 updating Element B while Thread 1 is doing a lock-free traversal.
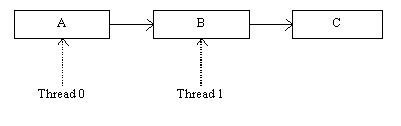
Figure 2: LIST INITIAL STATE
Suppose that Thread 0 needs to make a change to Element B that cannot be done atomically. Thread 0 cannot simply modify Element B in place, as this would interfere with Thread 1. Thread 0 instead copies Element B into a new Element B', modifies B', issues a memory-barrier operation, then points A’s next pointer to B'. This does not harm Thread 1 as long as B still points to C, and as long as Thread 0 waits until Thread 1 stops referencing B before freeing it.
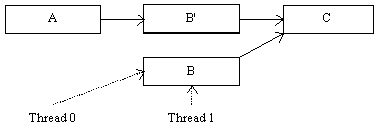
Figure 3: LIST DEFERRED DELETION
Thread 1 can no longer obtain a reference to B, so Thread 0 waits for a quiescent period (see Figure 4) before deleting it. After the quiescent period, Thread 0 deletes B, as shown in Figure 5.
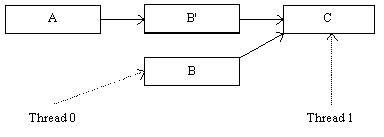
Figure 4: LIST AFTER QUIESCENT PERIOD
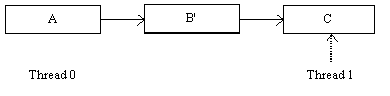
Figure 5: LIST AFTER DELETION
This idiom of updating a copy of an element while allowing concurrent reads gives "read-copy update" its name. This idiom may be easily extended to handle arbitrarily linked multi-lists.
Note that Thread 0 must use some sort of update discipline to handle concurrent updates. This update discipline can be of any sort, including explicit locking, atomic instructions, or techniques taken from wait-free synchronization [5]. However, if only one thread is allowed to update the data, all locking may be eliminated.
3.3.2 LOCK-FREE BUFFER FLUSHING
For another example, suppose that a parallel program creates log buffers that must be flushed to disk, but only after all log records have been completed. One approach is to maintain a global lock so that only one process at a time could create log records. However, this could result in a bottleneck under heavy load. Another approach is to use a global lock only to allocate space for the log records, and then create the actual records themselves in parallel. If the creation of a log record does not involve quiescent states, a flush may be safely initiated after a quiescent period starting after the last log record has been allocated.
Consider an initially empty two-entry log buffer:
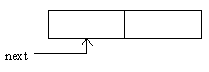
Figure 6: LOG BUFFER INITIAL STATE
If Threads 0 and 1 reserve both available slots, the situation will be as shown in Figure 7.
Both slots are occupied, and the "next" pointer is NULL. Therefore, Thread 2 must wait until Threads 0 and 1 have completed their entries, flush the log buffer, and only then reserve its slot.
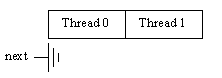
Figure 7: LOG BUFFER FULLY RESERVED
Threads 0 and 1 could use explicit synchronization operations to inform Thread 2 when they have completed their log entries. However, this would result in needless synchronization operations for log buffers with large numbers of entries. Instead, Thread 2 waits to flush the buffer until the end of the next synchronization period. This guarantees that Threads 0 and 1 have completed their entries without requiring synchronization operations.
Note that a garbage collector is not an appropriate solution for this second example, because we need to write out the log buffer instead of freeing it.
A thread is said to be in a quiescent state any time that it is not keeping prior state for any data structure. Many applications and systems have natural universal quiescent states, which are quiescent states that apply to all data structures in the application or system.
For example, within an operating system (OS) with non-preemptive kernel threads, there is a direct mapping from "thread" to CPU. Any CPU that is in the idle loop, executing in user mode, offline (halted), or performing a context switch cannot be holding any references to any kernel data structure. Therefore, each of these four states is a universal quiescent state.
Similarly, many parallel user applications drop all references to guarded data structures while waiting for user input. Many transaction-processing systems drop all references to guarded data structures at the completion of a transaction. Interrupt-driven real-time control systems often drop all references to guarded data when running at base priority level. Reactive systems often drop all references to application-level guarded data structures upon completion of processing for a given event. Discrete-event simulation systems often drop all references to guarded simulation data structures at the end of processing for each discrete event. These applications therefore also possess natural universal quiescent states.
Such systems will normally maintain statistics that track the number of times that they pass through their natural quiescent states. For example, most OSs will maintain counts of context switches and most transaction-processing systems maintain counts of the number of transactions complete. These counts, kept for performance-monitoring purposes, can be used to greatly reduce the cost of tracking quiescent periods, as will be shown in later sections.
3.5 SUMMARY OF THREAD ACTIVITY
Tracking quiescent periods is useful only if done very efficiently, otherwise, it is cheaper just to use locks. The mechanism that tracks quiescent periods is called a summary of thread activity. An efficient summary of thread activity is relatively complex, therefore, this section moves from simpler (but slower) implementations to more complex implementations suitable for large-scale shared-memory processing (SMP) and cache-coherent non-uniform memory-access (CC-NUMA) architectures.
For concreteness, we focus on a parallel non-preemptive OS. Therefore, the in-kernel threads map directly to CPUs, and the implementations focus on CPUs rather than threads.
The following sections describe the following implementations: (1) locking-primitive summary, (2) enforced quiescent states, (3) quiescent-state bitmask, and (4) quiescent-state counters.
3.5.1 LOCKING-PRIMITIVE SUMMARY
Perhaps the most straightforward way of identifying quiescent states is to maintain count of the number of locks held by each CPU. When this number drops to zero on a given CPU, that CPU records the fact that it has entered a quiescent state by clearing a its bit in a global bitmask. When the value of the bitmask becomes zero, the end of a quiescent period has been reached. Any subsystem wishing to wait for a quiescent period sets each CPU’s bit in the global bitmask.
Although this approach is simple, it is fatally flawed. First, it is slow, needing to update a global variable each time that a CPU releases its last lock. Second, update disciplines not using locks would have their critical sections violated by this sort of summary of thread activity. Finally, a CPU that ran for an extended period without acquiring any locks (e.g., a CPU in the idle loop) would never clear its bit, despite being in an extended quiescent state.
Therefore, a different approach is required.
3.5.2 ENFORCED QUIESCENT STATES
Another simple approach is to force quiescent states, for example, via a daemon that handles quiescent-period requests. The daemon responds to a request by running on each CPU in turn, then announcing the end of the quiescent period, as shown in Figure 8.
Each CPU that the daemon runs on must do two context switches, one to switch to the daemon, and the other to switch away. A context switch is a quiescent state, so this set of context switches is a quiescent period, as desired. In this case, the summary of thread activity is maintained as part of the local state of the daemon itself.
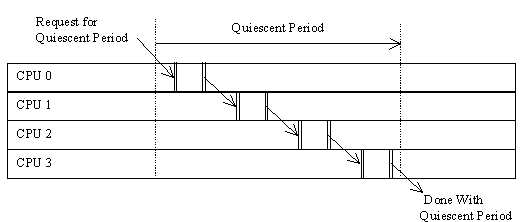
Figure 8: ENFORCED QUIESCENT STATES
This approach works well, and entered production on Sequent machines in 1993. Context switches are usually from one to three orders of magnitude more expensive than locking primitives, but for read-intensive data structures, the expense is justified. In addition, eliminating locks can greatly simplify deadlock avoidance. Furthermore, batching allows a single quiescent period to satisfy many requests.
Nevertheless, it is possible to do much better.
3.5.3 QUIESCENT-STATE BITMASK
Another approach is to instrument the quiescent states themselves. Each time a given CPU reaches a quiescent state, it clears its bit in a global bitmask. When the bitmask becomes zero, the quiescent state has ended. Any subsystem wishing to wait for a quiescent period sets each CPU’s bit in the global bitmask. A quiescent period measured in this manner is shown in Figure 9.
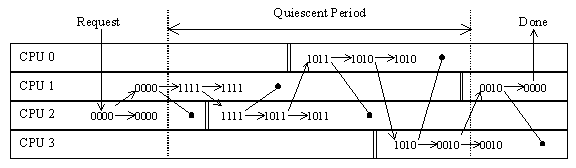
Figure 9: QUIESCENT-STATE BITMASK
CPU 1 has requested a quiescent period. The bitmask initially resides only in CPU 2's cache, so CPU 1 must first obtain a copy, as shown by the arrow. CPU 1 then writes all one-bits to the bitmask, invalidating the copy in CPU 2's cache, as shown by the line ending in a circle. CPU 2 is the first to pass through a quiescent period (shown by the double vertical line), so it gets a copy from CPU 1 in order to clear its bit, which invalidates the copy in CPU 1's cache. CPU 0 and CPU 3 pass through their quiescent states in a similar manner. Finally, when CPU 1 clears its bit, the bitmask becomes zero, indicating the end of the quiescent period.
To prevent long-running user-level processes and idle CPUs from indefinitely extending a quiescent period, the scheduling-clock interrupt handler records a quiescent state any time that it interrupts either user-mode execution or the idle loop.
This approach can be faster than enforced quiescent states, but the frequent accesses to the shared global bitmask can be quite expensive, as shown in Figure 10.
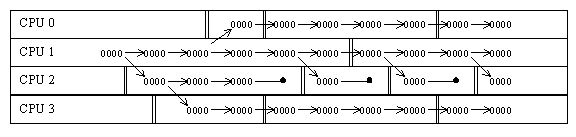
Figure 10: BITMASK CACHE THRASHING
CPU 2 is frequently forcing the bitmask out of its cache, thereby incurring expensive cache misses each time it passes through a quiescent state.
3.5.4 QUIESCENT-STATE COUNTERS
More-efficient implementations isolate measurement from callback processing. Quiescent states are counted per-CPU and subsystems wait for quiescent periods by registering callbacks on per-CPU callback lists.
An OS kernel's quiescent states either are counted anyway or occur when the CPU is not doing anything useful. Examples of the former include system calls, traps, and context switches. Examples of the latter include the idle loop and removal of CPUs from service. The pre-existing counts of these events are used to implement a quiescent-period-detection algorithm that incurs little added cost.
The basic outline of this algorithm is as follows:
An actual implementation faces these issues:
Our implementation of read-copy update uses quiescent-state counters. An SMP version has been in production in Sequent Dynix/ptx since 1994. The CC-NUMA version went into production in 1996 on a hierarchical-bus architecture with four CPUs per local bus. Each local unit is called a quad.
The four issues listed in the previous section are handled as follows:
4.1 STATE VARIABLES
The state variables for the quad-aware implementation of read-copy update are grouped into generation numbers, bitmasks, statistics, statistics snapshots, and callback lists.
Each quiescent period is identified by a generation number. Since the algorithm maintains loosely coupled state, there are several state variables tracking different generation numbers. The highest generation requested thus far is tracked by rcc_maxgen. The generation currently being serviced is tracked by rcc_curgen, which is replicated per-quad in pq_rcc_curgen. The earliest generation that a particular CPU needs to be completed is tracked by the per-CPU variable rclockgen.
The bitmasks track which CPUs and quads need to pass through a quiescent state in order for the current generation to complete. The set of quads that contain CPUs needing to pass through a quiescent state is tracked by rcc_needctxtmask, and the set of CPUs on a given quad needing to pass through a quiescent state is tracked by the per-quad variable pq_rcc_needctxtmask.
Each CPU tracks the number of context switches in the per-CPU variable cswtchctr. Each CPU tracks the number of system calls and traps from user mode in the per-CPU variables v_syscall and usertrap, respectively. Each CPU tracks the sum of the number of passes through the idle loop and the number of times a process to yielded that CPU in the per-CPU variable syncpoint.
As soon as a given CPU notes the start of a new generation, it snapshots its statistics: cswtchctr into rclockcswtchctr, v_syscall into rclocksyscall, usertrap into rclockusertrap, and syncpoint into rclocksyncpoint.
Read-copy callbacks advance through per-CPU callback lists nxtlist, curlist, and intrlist when quiescent periods are detected, as shown in Figure 11.
4.2 PSEUDO-CODE OVERVIEW
The pseudo-code call tree and function descriptions are as follows:
New callbacks are injected into the system by rc_callback(). While the callbacks are awaiting invocation by rc_intr(), they are kept on per-CPU linked lists, and flow through the system as shown in Figure 11. The rc_onoff() function moves callbacks to the global lists when a CPU is taken out of service. These global lists are processed in the same manner as the per-CPU lists.
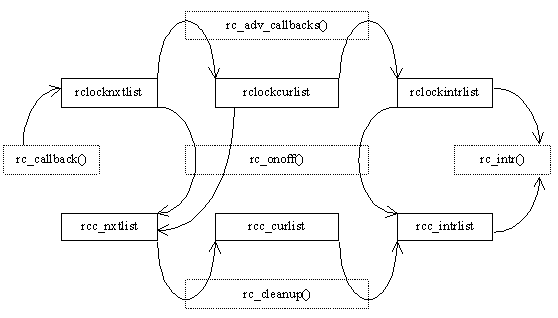
Figure 11: FLOW OF CALLBACKS
The actual implementation also includes functions to check for CPUs taking too long to reach a quiescent state. This pinpoints areas that are impacting real-time response.
Read-copy update performance depends on the fraction f of data-structure accesses that modify that data structure, and on the degree to which read-copy callbacks may be batched. Note that batching occurs naturally if several callbacks are registered during a single quiescent period. The ratio of read-copy update overhead to that of an uncontended simple spinlock is shown in Figure 12 for various batch sizes and for several relatively large values of f. These measurements were made on a Sequent NUMA-Q system [9] with 32 Intel Pentium Pro processors.
Note that all measurements taken with f=0.01 or less show that use of read-copy update results in large speedups compared to an uncontended simple spinlock. This low-contention case is the worst case for read-copy update. Under heavy contention, the overhead of simple spinlock rises dramatically, whereas heavy contention actually reduces the overhead of read-copy update due to batching. Further, as noted below, smaller values of f improve read-copy update performance. Finally, this data assumes multiple updating threads. A single updating thread would not need an update-side spinlock.
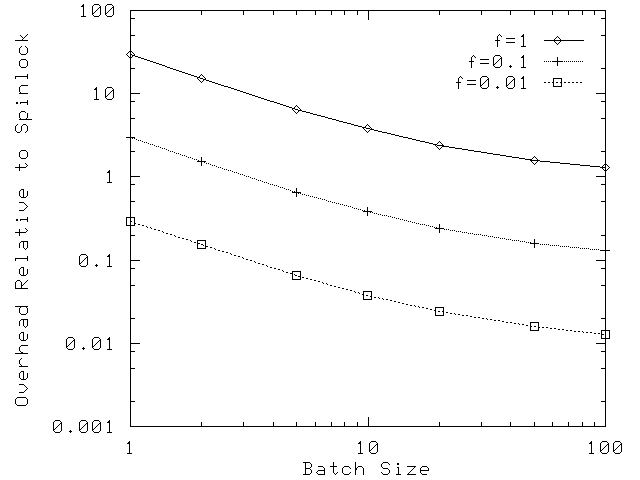
Figure 12: OVERHEAD OF READ-COPY UPDATE
Two examples will help to put the value of f in better perspective. The first example is a routing table for a system connected to the Internet. Many Internet routing protocols process routing changes at most every minute or so. Therefore, a system transmitting at the low rate of 100 packets per second would need to perform a routing-table update at most once per 6,000 packets, for f<10-3. The second example is a system with 100 mirrored disks, each of which has an MTBF of 100,000 hours. A transaction-processing system performing 10,000 disk I/Os per second would perform in excess of 1010 I/Os on the average before having to update the internal tables tracking which disk contains which data. This yields a value below 10-10 for f. In these cases, read-copy update vastly outperforms simpler locking schemes, since read-copy update overhead goes to zero as f approaches zero.
There are four components to read-copy-update overhead:
Equation 1, Equation 2, Equation 3, and Equation 4 give the read-copy
overhead incurred for each of these four components: per hardclock(), per
generation, per batch, and per callback, respectively:
|
Equation 1
|
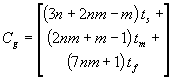 |
Equation 2
|
|
Equation 3
|
|
Equation 4
|
The worst-case cost of an isolated callback is m times the per-hardclock()
cost plus the sum of the rest of the costs, as shown in Equation 5:
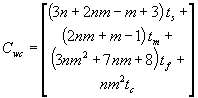 |
Equation 5
|
Typical costs may be computed assuming a system-wide Poisson-distributed
inter-arrival rate of l per generation,
as shown in Equation 6.
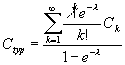 |
Equation 6
|
|
Equation 7
|
The expected number of batches Nb(k) is given by the
well-known solution to the occupancy problem:
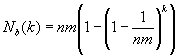 |
Equation 8
|
Substituting Equation 7 and Equation 8 into Equation 6 and substituting
Equation 1, Equation 2, Equation 3, and Equation 4 into the result yields
the desired expression for the typical cost:
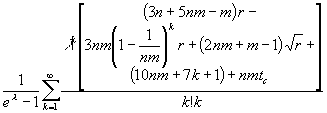 |
Equation 9
|
Figure 13 displays read-copy update overhead as a function of the number of CPUs. At these typical latency ratios and moderate-to-high update fractions, read-copy update outperforms the other locking primitives. Note particularly that the overhead of the non-worst-case read-copy overheads do not increase with increasing numbers of CPUs, due to the batching capability of read-copy update. Although simple spinlock also shows good scaling, this good behavior is restricted to low contention.
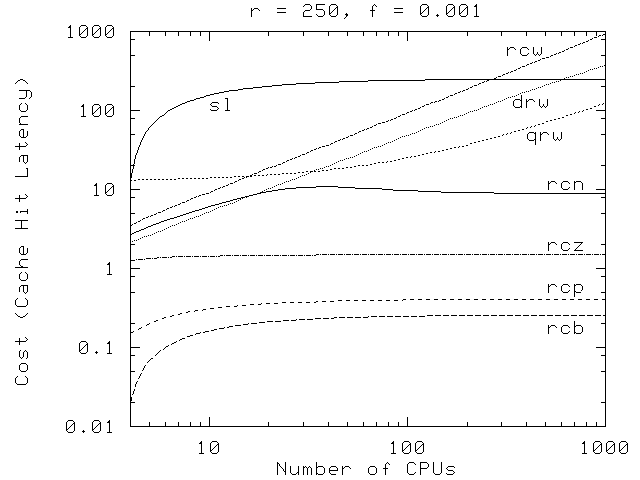
Figure 13: OVERHEAD VS. NUMBER OF CPUs
Figure 14 shows read-copy overhead as a function of the update fraction f. As expected, read-copy update performs best when the update fraction is low. Update fractions as low as 10-10 are not uncommon [13].
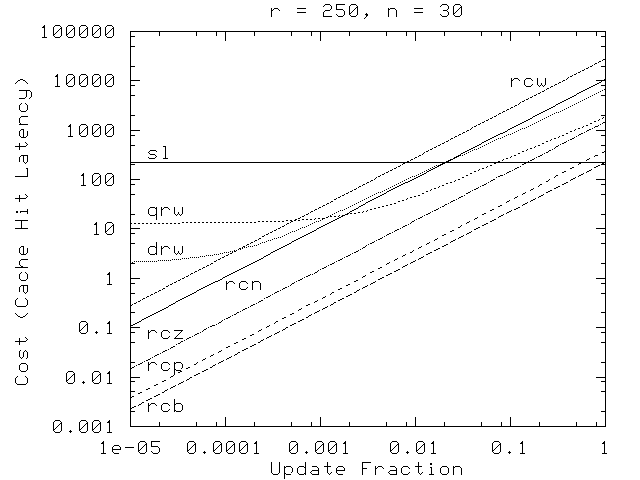
Figure 14: OVERHEAD VS. UPDATE FRACTION
Figure 15 shows read-copy overhead as a function of the memory-latency ratio r. The distributed reader-writer primitives have some performance benefit at high latency ratios, but this performance benefit is offset in many cases by high contention, by larger numbers of CPUs, or by lower update fractions, as shown in Figure 15
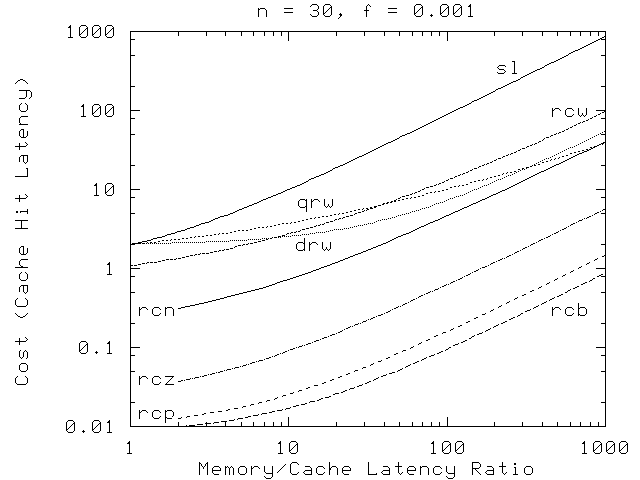
Figure 15: OVERHEAD VS. LATENCY RATIO
The situation shown in Figure 15 is far from extreme. As noted earlier, common situations can result in update fractions below 10-10.
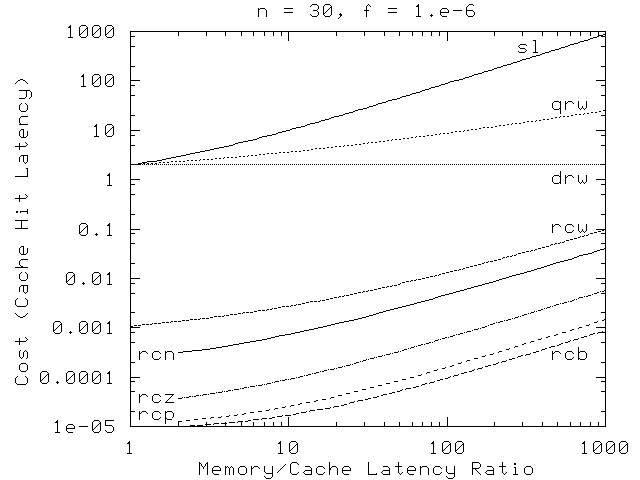
Figure 16: OVERHEAD VS. LATENCY RATIO FOR LOW f
Note finally that all of these costs assume that the update-side processing for read-copy update is guarded by a simple spinlock. In cases where the update-side processing may use a more aggressive locking design (for example, if only one thread does updates), read-copy update will have an even greater performance advantage.
Reader-writer spinlocks [14] allow reading processes to proceed concurrently. However, updating processes may not run concurrently with each other or with reading processes. In addition, reader-writer spinlocks exact significant synchronization overhead from reading processes. On the other hand, reader-writer spinlocks allow writers to block readers and vice versa, thereby avoiding stale data. This tradeoff is shown in Figure 17—exclusion between readers and writers imposes lock-contention costs and increases the time required to become aware of an external event.
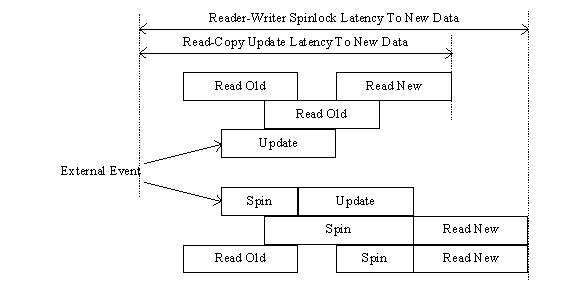
Figure 17: LATENCY OF READ-COPY UPDATE COMPARED TO READER-WRITER SPINLOCK
Wait-free synchronization [5] allows reading and updating processes to run concurrently, but again exacts significant synchronization overhead. It also requires that memory used for a given type of data structure never be subsequently used for any other type of data structure, and that reading threads write to shared storage. On parallel computers, these writes will result in high-latency cache misses. On the other hand, wait-free synchronization provides wait-free processing to updates as well as to reads, and also avoids stale data.
Timestamping and versioning concurrency-control is in some ways similar to read-copy update, but imposes synchronization overhead on reading processes [2]. Chaotic relaxation [1] accepts stale data to reduce locking overhead, but requires highly structured data.
Manber and Ladner [10] describe an algorithm that defers freeing a given node until all processes running at the time the node was removed have terminated. This allows reading processes to run concurrently with updating processes, but does not handle non-terminating processes such as those found in OSs and server applications. In addition, they do not describe an efficient mechanism for tracking blocks awaiting deferred free.
Pugh [15] uses a technique similar to that of Manber and Ladner, but notes that (expensive) read-side state update can handle non-terminating processes. However, Pugh leaves to the reader the mechanism for efficiently tracking blocks awaiting deferred free.
Kung and Lea [7, 8] describe use of a garbage collector to manage the list of blocks awaiting deferred free. However, garbage collectors are often not available, and their overhead renders them infeasible in many situations. In particular, the traditional reference-counting approach incurs expensive memory writes for reading threads. Even when garbage collectors are available and when their overhead is acceptable, they do not address situations where some operation other than freeing memory is to be performed in a timely manner at the end of the quiescent period.
Jacobson [6] describes perhaps the simplest possible deferred-free technique: simply waiting a fixed amount of time before freeing blocks awaiting deferred free. This works if there is a well-defined upper bound on the length of quiescent periods. However, longer-than-expected quiescent periods (perhaps due to greater-than-expected load or data-structure size) can result in memory-corruption failures, with no feasible means of diagnosis.
We have presented a novel update discipline, named read-copy update, that provides great reductions in synchronization overhead, tolerates non-terminating threads and reduces deadlock-avoidance complexity. Read-copy update generally gives the best performance improvement for read-mostly algorithms or under high contention. In some cases, the need for synchronization operations is completely eliminated.
We have delineated read-copy update’s area of applicability: Data structures that are often accessed and seldom updated, where a modest amount of memory may be spared for structures waiting on a quiescent period, and where stale data may be tolerated or can be suppressed.
We have provided a firm theoretical basis for read-copy update, along with a very efficient implementation. This implementation, which uses a summary of thread activity, fills an important gap in earlier work with concurrent update algorithms. The implementation has run in production on Sequent machines since 1994.
We have presented measurements that demonstrate order-of-magnitude reductions in overhead compared to simple spinlock. These comparisons are quite conservative: even greater savings would be realized if the simple spinlock were heavily contended.
ACKNOWLEDGEMENTS
We owe thanks to Stuart Friedberg, Doug Miller, Jan-Simon Pendry, Chandrasekhar Pulamarasetti, Jay Vosburgh and Dave Wolfe for their willingness to try out read-copy update, and to Ken Dove, Brent Kingsbury, and to Phil Krueger and his Base-OS Reading Group for many helpful discussions. We are greatful to Dale Goebel, Dave Stewart, John Cherry, and Hans Tannenberger for their support of this work.
This work was done with the aid of Macsyma, a large symbolic manipulation program developed at the MIT Laboratory for Computer Science and supported from 1975 to 1983 by the National Aeronautics and Space Administration under grant NSG 1323, by the Office of Naval Research under grant N00014-77-C-0641, by the U. S. Department of Energy under grant ET-78-C-02-4687, and by the U. S. Air Force under grant F49620-79-C-020, between 1982 and 1992 by Symbolics, Inc. of Burlington Mass., and since 1992 by Macsyma, Inc. of Arlington, Mass. Macsyma is a registered trademark of Macsyma, Inc.
REFERENCES
[1] Gregory R. Adams. Concurrent Programming, Principles, and Practices, Benjamin Cummins, 1991.
[2] N. S. Barghouti and G. E. Kaiser. Concurrency control in advanced database applications, ACM Computing Surveys, September 1991.
[3] Doug Burger, James R. Goodman, and Alain Kägi. Memory bandwidth limitations of future microprocessors, ISCA’96, (May 1996), pages 78-89.
[4] John L. Hennessy and Norman P. Jouppi. Computer technology and architecture: An evolving interaction. IEEE Computer, page 18-28, Sept. 1991.
[5] Maurice Herlihy. Implementing highly concurrent data objects, ACM Transactions on Programming Languages and Systems, vol. 15 #5, November, 1993, pages 745-770.
[6] Van Jacobson. Avoid read-side locking via delayed free, private communication, September, 1993.
[7] H. T. Kung and Q. Lehman. Concurrent manipulation of binary search trees, ACM Trans. on Database Systems, Vol. 5, No. 3 (Sept. 1980), 354-382.
[8] Doug Lea. Concurrent Programming in Java, Addison-Wesley, 1997.
[9] T. Lovett and R. Clapp. STiNG: A CC-NUMA computer system for the commercial marketplace. In Proceedings of the 23rd International Symposium on Computer Architecture, pages 308-317, May 1996.
[10] Udi Manber and Richard E. Ladner. Concurrency control in a dynamic search structure, ACM Trans. on Database Systems, Vol. 9, No. 3 (Sept 1984), 439-455.
[11] Paul E. McKenney. Selecting locking primitives for parallel programs, Communications of the ACM, Vol. 39, No. 10 (1996).
[12] Paul E. McKenney. Comparing performance of read-copy update and other locking primitives, Sequent TR-SQNT-98-PEM-1, January 1998.
[13] Paul E. McKenney. Implementation and performance of read-copy update, Sequent TR-SQNT-98-PEM-4.0, March 1998.
[14] John M. Mellor-Crummey and Michael L. Scott. Scalable reader-writer synchronization for shared-memory multiprocessors, Proceedings of the Third PPOPP, Williamsburg, VA, April, 1991, pages 106-113.
[15] William Pugh. Concurrent Maintenance of Skip Lists, Department of Computer Science, University of Maryland, CS-TR-2222.1, June 1990.
[16] Michael L. Scott and John M. Mellor-Crummey, Fast, contention-free combining tree barriers, University of Rochester Computer Science Department TR#CS.92.TR429, June 1992.
[17] John D. Slingwine and Paul E. McKenney. System and Method for Achieving Reduced Overhead Mutual-Exclusion in a Computer System. US Patent # 5,442,758, August 1995.
[18] Harold S. Stone and John Cocke. Computer architecture in the 1990s. IEEE Computer, pages 30-38, Sept. 1991.