Mountain Bike Rear Suspension Design
| Index |
| Introduction |
I assume if you've found this page your search has found many others. You've probably already read various manufacturer's vaguely technical marketing blurbs about why their suspension is the best. You've probably also read some of the more independent, though not necessarily less biased, discussions in various forums. I personally find these discussions both insufficiently detailed and overly detailed. All the overviews of how different suspensions work that I've seen fall short of getting into actual physics. Most of the detailed discussions I've come across are devoted to niche aspects of suspension design or vehement statements of personal preferences. Both tend to make a lot of fuss over relatively minor differences.
The one exception I've encountered is Ken Sasaki's Path Analysis, which is by far the most rigorous investigation of bicycle suspension I've found. It also happens to be the most readable. If you're looking for a dissection of suspension design that's both broad and detailed, there doesn't seem to be anything else like it; the rest of the suspension discussion on this page assumes familiarity with Sasaki's work. To summarize, Sasaki's conclusions are
Sasaki's analysis omits sweet spot unified rear triangle (URT) and floating bottom bracket (FBB) designs and therefore doesn't investigate what happens when the pivot location lies well above the chainrings. The best treatment of such very high pivot suspensions I've come across is Mike Padilla and Joe Brennan's Bicycle Rear Suspension Study. Their analysis reaches one very important conclusion. Namely
In situations where path analysis applies, any instantaneous pivot point which produces the same path tangent as a top tube pivot will have sufficient anti-squat to zero out pedaling forces. However, Padilla and Brennan neglect riders' weight shifts while pedaling and therefore overestimate the optimum pivot height; it's probably closer to a sweet spot URT than a top tube pivot. Common rear suspension frames like monopivots, four bars, and faux bars—which, as a class, are referred to here as unified front triangle (UFT) designs—are all capable of having this much anti-squat. The problem is moving the rear axle back that quickly causes a rapid increase in chain length, which in turn produces significant pedal feedback and problems the chain coming loose. As a result, all UFT frames end up having insufficient anti-squat to cancel pedaling forces. Investigation with Gergely Kovacs' Linkage shows it's possible to modify a VPP unified front triangle frame like the Santa Cruz Blur or Rocky Mountain ETSX to have sufficient anti-squat around the set point and then send the pivot point forward as the suspension compresses for better large bump response. Unrealistically tight frame tolerances are required, chain growth is significantly higher than the de facto limit of 15mm over the first 80mm of suspension travel, and the pivot remains far enough back in the frame large bump response would be poor. A more even handed tradeoff between anti-squat and bump response is the DW Link, which lacks sufficient anti-squat to avoid bob. It therefore seems the behavior associated with top tube and sweet spot pivots is implementable only in URTs or FBBs.
As of this writing, almost all rear suspensions are UFTs. URTs were all the rage in the mid-1990s but have since fallen out of favor because, within the range of pivot positions feasible in a UFT design, a UFT outperforms a URT. The Klein Mantra, the only commercial top tube pivot frame ever made, went out of production in 2001. Sweet spot URTs, such as the Schwinn Homegrown and Ibis Szazbo, are also discontinued. Maverick's line of bikes, all quite expensive, essentially is the FBB market. Everything else is a UFT, including the GT iDrive. So the only way to avoid pedal bob in a frame you can buy off the shelf today is to use a rear shock which provides a pedaling platform. Thus, barring significant innovation in rear triangle linkages or a reintroduction of a sweet spot frame, UFT frames using pedal platform shocks to control bob are here to stay.
As a rider, all this means practical differences between rear suspension frames within a given class of riding, such as XC or all mountain, are relatively small. Different pivot placements offer different bump response, different degrees of pedal feedback, and different amounts of anti-squat. But you can only have two out of those three things, and making any one of them better involves making something else worse. Since most frames make similar suspension compromises, variables like fit and geometry matter as much or more in choosing a bike as the suspension design. Hence, Sasaki's advice to go test ride a bunch of bikes and pick the one you like best is well taken.
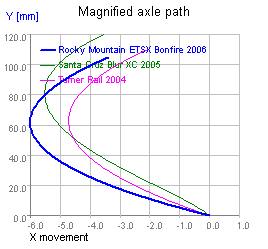
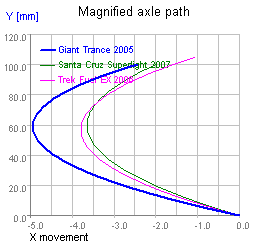
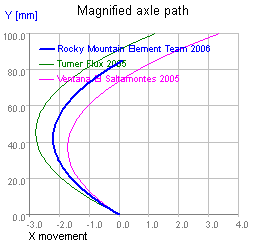
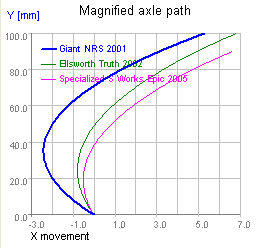
From a frame engineering standpoint it's hard to do anything significantly different from some UFT bike that's already out there. The primary opportunity for innovation is most likely greater pivot point agility in VPP suspensions but, given the wide availability of platform rear shocks, the value of building anti-squat into a frame is unclear. Similarly, chain growth limits rearward axle movement in UFTs, so it's difficult to produce a frame whose rear axle path will stand out from other UFTs. The four figures below show the range of typical UFT axle paths, progressing from the most rearward to the most forward. Over the first 100 mm of travel, the paths vary less than 6 mm from vertical and are therefore bounded within a wedge about 10° wide. This is a relatively constrained design space, though some riders exhibit very strong preferences for particular parts of it.


While having something different about a bike is certainly good source material for marketing it doesn't change physics; Sasaki's path analysis results are general enough to apply to all bikes. The only way to escape path analysis's range of validity is to make the mass of the swingarm large compared to the overall mass of the rider and bicycle. And the only viable way to do that is to put the rider's mass on the swingarm by making the bike a URT and having the rider stand. It's well known this situation causes the rear suspension to become less active, and the resulting "lockout" is the primary reason riders have rejected URTs. As has been pointed out innumerable times, standing usually means the rider's either climbing steeply or descending and virtually all riders prefer a suspension that's active in these situations. Ironically, the resulting dominance of UFTs means URTs' behavior with a standing rider is not well understood. Similarly, high pivot URTs tend to get lumped in with URTs whose pivots in positions are accessible to UFTs, obscuring the considerable sophistication of sweet spot URT design. In the interests of extending Sasaki's UFT focused work to encompass all frame designs, the next section examines these two situations more closely, along with some of the more obscure advantages of high pivots. Those results are then combined with Path Analysis to describe FBB behavior. Chain growth and braking, two other areas where Sasaki's treatment lacks depth are discussed, as well.
| Acknowledgements |
A special thanks to Gergely Kovacs for fixing a few bugs in Linkage and releasing Linkage 2.5 Upgrade 4—among other things, a couple of the figures here use features added in that release—as well as peer reviewing much of this page.
| High Pivot URTs |
Klein made Mantras from 1997 to 2001. A similar class of URTs, patented by John Castellano and produced around the same time as the Mantra by Schwinn and Ibis, is known as sweet spot designs. As noted above, these designs have pivot placements which are too high to be feasible in a UFT. Padilla and Brennan's suspension study, linked above, provides an introduction to what happens as the pivot point is moved well above the chainrings and shows how a high pivot location provides enough anti-squat to significantly or completely cancel pedaling forces. They don't mention names, but the upper bike on page eight of their paper is a Mantra and the lower one is a Schwinn Homegrown. Sasaki provides an introduction to how bump and drop off forces interact with suspensions as well as a look at how anti-squat counteracts pedaling forces in chapter III of Path Analysis, but doesn't consider sweet spot or top tube pivots. As Sasaki's already established, a UFT and URT with the same pivot placement have the same behavior when the rider is seated, so the primary results of this section are 1) the bottom bracket path controls URT behavior when the rider is standing and 2) the path can be varied to produce behavior anywhere from that of a UFT to that of a hardtail. These bottom bracket effects are intimately related, but are commonly cited as two different problems. One is the suspension becomes less active when the rider stands on the pedals. The other is the bottom bracket moves relative to the seat.
In chapter V of Path Analysis, Sasaki points out a URT and a UFT with pivots a mathematically small delta away from the bottom bracket have identical behavior. Another way of thinking about it is a bike with a pivot at the bottom bracket is both a URT and UFT at the same time. So, in the limiting case where there is no bottom bracket path, a URT remains fully active with a standing rider the way a UFT does. The other extreme of the URT design space is a pivot at the rear axle, commonly known as a hardtail, which can be thought of as reducing the swingarm to zero length and stretching out the front triangle so the rider's motion is fully coupled to rear wheel motion. The figure below, similar to the ones in chapter III of Path Analysis, shows an idealized model of a swingarm with some amount of rider mass on it and should help in visualizing how the motion of the rider mass varies based on its position along the swingarm. How much of the rider's mass is associated with the swingarm depends on what the rider's doing. Climbing out of saddle will couple nearly all of the rider's mass to the swingarm. Descending with knees bent for shock absorption will couple less. How much the suspension deactivates is a function of both the amount of rider mass on the swingarm and the path of the bottom bracket.
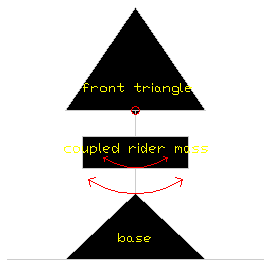
Like UFTs, URTs have a special point theory. The URT version holds the suspension remains fully active when the bottom bracket is directly below the pivot because the rider's weight doesn't exercise any torque on the swingarm. Like other special point theories, this is in the right direction but wide of the mark. As Sasaki again points out, this time in chapter II's discussion of forces and torques, suspension theories which don't take into account mass distribution will be incorrect. If the swingarm moves, rider mass on the swingarm must also move. Therefore an additional amount of energy, proportional to the amount of coupled rider mass, is required to move the swingarm. So the suspension cannot be as active as it is without rider mass on the swingarm. This holds true for any non-UFT pivot placement. At the suspension's sag point, a first order approximation of the force a bump exerts on a URT swingarm with a standing rider is
Fb = mrcalr + mrcglrsin(q)) + msa
where mrc is the rider mass coupled to the swingarm, a is the acceleration of the rear axle, lr is the suspension's leverage ratio, g is the acceleration of gravity, q is bottom bracket path angle relative to gravity, and ms is the swingarm's mass. (The smaller Fb is the more active the suspension; ideally Fb = 0 so that the suspension flows effortlessly over obstacles.) URT special point theory targets q = 0 or 180° to obtain sin(q) = 0 to zero the second term, but a glance at the equation shows the optimum case will be somewhere in the range of 180 < q < 360° so that second term of the equation goes negative and cancels as much of the first and third terms as possible. The optimum path angle varies as a function of all other terms on the right hand side of the equation and full cancellation typically becomes impossible someplace around a = 0.8g. To put it in mundane terms, what the equation is saying is if compressing the suspension lowers rider mass the resulting liberation of gravitational potential energy makes it easier to for a bump to move the swingarm. In practice this is difficult to take advantage of because lowering rider mass requires the pivot be located behind the bottom bracket. Most low pivot URT designers therefore seem to have settled for minimizing lr by placing the pivot near, but in front of, the bottom bracket. lr is the ratio between the rear axle and bottom bracket's instantaneous displacements. lr varies between about 0 and 0.6, with 0 corresponding to an ideal UFT with a massless swingarm and 0.6 being a hardtail pivoting about the front axle as the rear wheel goes over a bump. In an ideal URT with a massless swingarm and zero coupled rider mass the swingarm is the only part of the frame which moves in response to a bump. However, as mrc increases rider mass transfers from the front triangle to the swingarm. Given an ideal, massless URT frame, the bike will behave like a hardtail when mrc is equal to the total rider mass. With a partial transfer of rider mass then the frame's motion over the bump is a combination of swingarm compression and hardtail motion. A first order approximation for lr is then
lr = ls + mrc (lht - ls) / (mr + mft)
where ls is the leverage ratio of the swingarm, lht the leverage ratio of a hardtail with the same geometry as the URT frame, mr the rider's total mass, and mft the mass of the front triangle. ls is the bottom bracket to pivot distance divided by the rear axle to pivot distance. A typical low pivot URT has an ls of about 0.1 and the Mantra is 0.58.
The model above can be used to provide an estimate of how locked out a URT becomes when the rider stands. It probably makes most sense to define lockout as the ratio of a URT's bump force to the bump force on a hardtail. This deactivation ratio is roughly
dr = (mrcalr + mrcglrsin(q)) + msa) / (lht (mra + mrgsin(q)) + mba))
where mb = mft + ms is the bike's total mass. There are three motivations for using a force ratio. One is the rear axle displacement caused by a bump is dominated by the size and shape of the bump along with size and inflation of the rear tire and is a weaker function of the suspension design. Second, the angular rotation of the swingarm depends on the reference point chosen as well as the amount of front triangle motion and compression in the front fork. Third, when measuring a suspension's ability to respond to bumps what matters is the size of the bump force, not the actual motion of the suspension. The direction of the force a bump exerts on the rear wheel depends on the shape of the bump, where it hits the bike, and even how fast the bike hits it, but since the rear wheel mostly free to rotate a reasonable approximation is the force is tangential to where the bump hits the wheel. While this is a very simple model, in my experience it agrees tolerably well with what actually happens on the trail. The figure below shows the tangential forces for a series of up bumps, each 2.5 cm taller than the last.

Note all the bumps push back on a bike as well as up. The bigger the bump force, the larger the amount of backwards push and the more the bike will slow down in response to a bump. Similarly, the bigger the bump, the more backwards push. Suspension designers can't change how much mass a rider puts on a URT swingarm or what bumps the rider will go over, so their best option for maximizing suspension efficiency is to make the bump force as small as possible (the next best option is to reduce the backward component of the bump force by making the wheel bigger, e.g. a 29er). Since dr goes to zero when the bump force does, dr provides a direct measure of a suspension's efficiency in handling bumps. It also provides a direct measure of how much force the rider feels on the parts of their body coupled to the swingarm, and therefore provides an estimate of rider comfort. It's difficult to be precise about the quantities in the equation and there is no established definition of lockout, so the definition of dr is approximate. Since ms ~ lrmb, dr ≈ lrmrc / (lhtmr), which varies between 0 and 1 as a function of mrc. For URT frames with pivots near the bottom bracket, dr increases proportional to mrc2. For URT frames with top tube pivots, dr is linear with lr. However, for dr ≈ 1 for both types of frames when mrc = mr. Low pivot URTs are therefore more active than high pivot URTs in the neighborhood of mrc = 0.5 mr but under this model for lr there is not a major difference between the two pivot locations when mrc is small or large. More sophisticated treatment of lr may show dr → 0 as ls → 0; at this level of detail it's not clear if a discontinuity should exist at ls = 0.
Two of the equation quantities are worthy of additional comment.
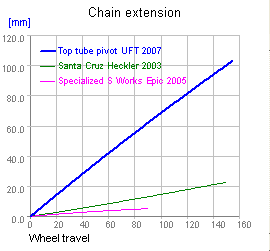
Since dr ≈ mrclr / mr, a rider experiences somewhere between perhaps 25% and 50% of the bump force they'd feel on a hardtail, depending on mrc and lr. So even a "locked out" URT is less bumpy than a hardtail. However, the bump force in a UFT is only msa, which translates to a dr around 2%. For out of saddle riders, URT bump forces are still far higher than in a UFT. Lacking cranks and a bottom bracket, a UFT swingarm will be around half the mass of a URT swingarm and some of the mass of a URT rider's feet will be coupled to the swingarm even when the rider is seated. dr is perhaps 4% for an on saddle rider on a URT. In short, if you don't mind a little chain growth, there's no compelling reason to use a low pivot URT instead of a UFT. High pivot URT designs, however, offer cancellation of rider pedaling forces and the best available bump response at the expense of a more hardtail like behavior when rider weight is off the saddle. (A UFT frame with a top tube pivot isn't viable is it would have 65 mm of chain extension at 80 mm compression. In comparison, a typical UFT has around 7.5 mm of chain growth and maybe 10 degrees of pedal feedback. Designs like the Santa Cruz Heckler, which puts the pivot well forward and high up by UFT standards, have about 12 mm of growth and are still under 20 degrees of feedback. Alternatively, one could raise the bottom bracket in a UFT about 75 cm, but the resulting bike would be unrideable for practical purposes.)
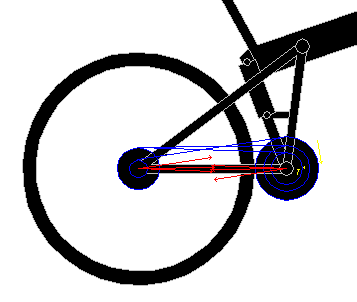
An astute reader will notice a contradiction between Sasaki's result in chapter II of Path Analysis and Padilla and Brennan's results. Sasaki says there is no pivot placement which cancels a rider's pedaling forces in all gears. Padilla and Brennan say there is, provided one assumes a URT's suspension is independent of chain forces. In chapter V of Path Analysis Sasaki shows that, contrary to popular belief, URT suspensions are not independent of chain forces. What Sasaki doesn't spell out is chain induced forces within a URT's rear triangle cancel and the torques largely cancel. It's the residual torque which activates the suspension in response to pedaling. The closer in size the chainring and cog in use are, the smaller the residual. The figure below shows the chain forces on a Mantra's rear triangle in red, along with yellow arrows pointing in the direction of the suspension movement. The yellow arrows' size depicts the relative magnitudes of the torque residuals, under the unlikely assumption the rider pedals equally hard in all gears. Back of the envelope calculations suggest the largest residual is in the range of 1 or 2 Nm when a typical rider is pedaling hard, which translates into something like a 75 N variation in the load on the shock. In comparison, the preload on the shock is around 1.5 kN and the Mantra usually runs something like 10 mm of sag. So the 5% worst case variation in shock loading produces about 0.5 mm of suspension bob in an ideal, frictionless, world. More typical gearing combinations and pedaling effort produce amounts of suspension bob measured in microns and, in reality, shocks and pivots have friction.
So, while Sasaki is certainly correct, Padilla and Brennan's assumption of independence from chain forces is an excellent approximation. What matters in practice is how close the top tube pivot placement comes to actually canceling the rear wheel and pedal torques. What Padilla and Brennan fail to consider in their study is the force a rider exerts on a pedal has to come from somewhere. When the rider is seated, any net downward force applied to the pedals reduces the amount of rider weight on the saddle. The net effect is the load the rider exerts on the suspension moves forward, reducing the force on the rear shock and increasing the force on the front shock. If a top tube pivot URT is set up with sag, this weight transfer causes the swingarm to extend. Suspensions in this configuration are more prone than usual to bob since pedaling extends the rear shock rather than compressing it. Four things can be done about this. In roughly decreasing order of desirability, they are
Besides controlling pedaling forces, the other advantage of a high pivot location is better bump response. The figure below with swingarm paths for the Mantra, Epic, and Heckler clearly shows how far from the UFT design space a top tube pivot URT is. The rear axle trajectory on the Mantra is about 120°, while the Epic and Heckler are more or less vertical. Recall the figure above showing approximate bump force vectors and note that for bumps smaller than 8 cm or so the bump force angle in an up bump is also about 120°. This means typical up bumps try to push the Mantra's swingarm in the direction it would naturally move, whereas UFT linkages are restricted to moving upwards even though the bump is trying to push the axle back.
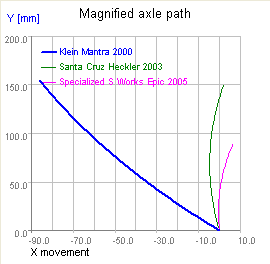
More formally, the amount of bump force which goes into compressing the suspension is the dot product of the wheel force and a unit vector representing the suspension's instantaneous angle of travel. Any up bump force which doesn't compress the suspension either pushes the bike backwards or lifts the bike, both of which act to reduce the bike's kinetic energy and are felt by the rider. A design which aligns suspension travel with bump force transmits virtually all bump energy into the rear shock. With the vertical pivot trajectory typical of most UFTs or low pivot URTs about 85% of the bump energy goes into the shock. The other 15% goes into slowing the bike down. Assuming an equal fraction of energy is lost to damping in the rear shock, a top tube pivot recovers about 20% more of the energy lost to the bump than a good UFT. And, as a side effect, provides a more comfortable ride. How much of a difference this makes depends on how many bumps there are and is hard to gauge, but differences in how suspensions respond to bumps are definitely perceptible to riders. This effect is, however, relatively small compared to the range in shock rates. An additional advantage of a high pivot location is the suspension's rearward movement increases the amount of time a suspension has to respond to a bump, thereby reducing the acceleration needed to move the swingarm out of the bump's way and, in turn, reducing the bump force. (The numerical integrations to determine how much the bump force changes aren't that difficult but, lacking Linkage Professional and detailed shock information, I lack the ability to export good force data to base the integrations on.)
The flip side of a high pivot location is the suspension isn't as active on drops. This is largely an academic point, since taking rider weight off the saddle is has a much larger effect. When landing a drop the "bump" force on the rear wheel is more or less vertical. Given sufficient speed, any down bump turns into a drop. The more or less vertical path of a UFT results in a suspension whose behavior doesn't differ much between an up bump pushing back and a drop pushing straight up. Tilt the axle path backwards with a high pivot to better absorb up bumps and the suspension won't be as active in compressing in response to the drop. The result is a slightly more pronounced impact at the bottom of the bump. If the bike is moving slowly enough for the rear wheel to track the down bump, the tangential forces of the bump push forward and up instead of backwards and up as they do in a down bump. It's unclear if a low or high pivot works better in this situation; what matters is the suspension's ability to extend through its sag to proactively absorb the down bump. Suspension setup seems to matter more in this case than choice of pivot location..
Besides being less active when the rider is off the saddle, the other drawback of URTs is bottom bracket motion relative to the
seat. The suspension effects are discussed above, but it's worth
mentioning one other effect rider on the rider. To review, the greater the distance between the bottom bracket and pivot the
greater the the bottom bracket's motion will be. A top tube pivot therefore has
the greatest bottom bracket motion, with the Mantra moving back and up 38 mm relative to the seat in the first 80 mm of travel.
The bracket moves about 80 mm before the rear suspension bottoms out around 165 mm
compression, though it's rare to hit a cross country frame this
hard. While changing seat to pedal distance is often seen as undesirable when approached from a theoretical
standpoint, moving the bottom bracket back 30 mm or so from the suspension's set
point is roughly equivalent to a rider scooting forward on the seat a bit to get more
power while climbing. A suspension which helps the rider power away from a bump is no bad
thing, though it is certainly possible to feel the pedals move as the
suspension compresses if you're paying attention. It drives some people
nuts, and a few others find it conceptually offensive, but most riders say they
don't
notice the bottom bracket moving after the first couple rides. So the Mantra's bottom bracket's
motion isn't too much of a problem in practice. A related effect, whose value is hard to quantify, is
moving the rear axle back as the suspension compresses lengthens the
wheelbase. In principle, having a
bike which becomes more stable the more it gets bounced around is no bad thing,
but in practice most riders don't seem to notice the handling change.
| Floating Bottom Brackets |
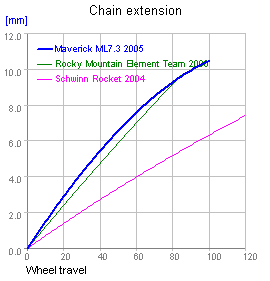
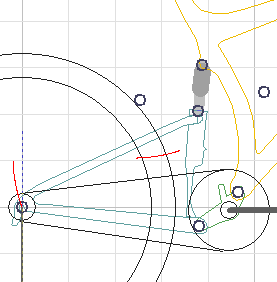
This section is brief, for the simple reason floating bottom bracket designs are linkage URTs. From the discussion of URT behavior above, it should be clear bump forces are a function of the amount of rider mass coupled to the swingarm. Since floating bottom bracket linkages place the bottom bracket on the swingarm, rider mass will be coupled to a FBB swingarm when the rider is standing and the suspension will become less active. The discussion above about the effects of URT placement relative to the bottom bracket makes no assumption about what sort of linkage is used to realize the swingarm and is therefore general to FBBs as well as URTs. Like linkage UFTs, FBB linkages remove the constraint a swingarm's center of curvature be a physical pivot. This creates interesting theoretical possibilities, such as producing a sweet spot pivot location with some other kind of frame, but experimentation in Linkage suggests FBBs converge towards URTs as pivot locations move out of the UFT space. Thus, the primary value of an FBB is more control over how much chain growth occurs. One edge of the FBB design space is the UFT case, where bottom bracket doesn't move as the rear axle moves. The other end is the URT case, where the bottom bracket motion is such the distance between the bottom bracket and rear axle remains constant. A bottom bracket bearing linkage allows a pivot point which pushes the limits of acceptable UFT chain growth while allowing \bottom bracket motion to reduce the amount of pedal feedback. The two FBBs currently on the market, Maverick's and Schwinn's, do exactly this. Both use higher pivot locations than can be achieved with a UFT but have chain growth figures comparable to a typical UFT. For the Rocket, ls ≈ 0.36. Both frames have pivots well below the top tube, so the Schwinn's advantage over a top tube pivot URT, which will have ls ≈ 0.6, is not clear cut. The Maverick ML7 obtains ls ≈ 0.09 with a pivot location higher than is possible in a URT frame with comparable ls. However, as shown in the figure at right below, the effective pivot point is relatively far back in the frame and moves farther back as the suspension compresses. So, while an FBB can provide design points between a UFT and URT, current linkages appear to make relatively expensive compromises between a high pivot placement and maintaining a low ls.
| Chain Growth and Braking |
A favorite marketing technique is to proclaim a suspension fully active. Presumably, a fully active suspension is one whose ability to absorb bumps is not affected by pedaling, braking, or rider position. Sasaki's discussion of all three of these issues is minimal. As discussed above, URTs fail the rider position criteria. UFTs are sensitive to rider position as well, though not enough so for it to be a significant issue. This section therefore focuses on pedaling and braking. Sasaki discusses pedaling in considerable detail and clearly notes the tradeoffs between anti-squat, chain growth, and bump absorption. To summarize, providing anti-squat to mitigate bob requires the tighter path curvatures of pivots positioned well back in the frame in order to limit chain growth. As Sasaki points out and as discussed above, moving the pivot rearward reduces the quality of bump response. But Sasaki does not complete the argument. Sweet spot URTs are least affected by pedaling. Path analysis states suspensions with identical path tangents have identical behavior, so any pivot placement along the line between the rear axle and the pivot of a sweet spot URT will offer similar insensitivity to pedaling. Since this line passes above the bottom bracket, any useful UFT pivot placement along the line will cause chain growth as the suspension compresses. While alternative transmissions like the G-Boxx modify this constraint, it remains the vast majority of frames must trade off pedaling effects for avoiding chain growth. This makes it unclear what constitutes a fully active UFT. If the designer avoids chain growth the bike will bob, varying the compression of the suspension and therefore varying the suspension's ability to respond to bumps. If the designer tries to minimize bob, chain growth occurs. Tension in the chain means swingarm movement requires energy proportional to the total increase in the chain's effective length, so the suspension cannot have the same bump response during pedaling as when there is zero chain tension. Given equivalent bump responses, a UFT with lower chain growth will be more efficient in this regard than a UFT with greater chain growth. However, there is no such thing as an equivalent bump response. Rotating the path tangent to decrease chain growth increases energy loss to bumps as well as bob. Whether a low chain growth or a high chain growth suspension is more efficient overall depends on the rider, the bumps, and the suspension tuning. Rigorous answers require dynamic analysis well beyond the simple approaches used in this page, but back of the envelope analysis shows bump and pedaling forces are of comparable magnitude. Efficiency gains from reduced chain growth are therefore likely to be cancelled by the increased bump energy loss over the 7.5° path angle spread between low and high chain growth URTs. Fortunately, rider behavior tends to limit energy loss to chain growth. Riders usually don't pedal through big bumps and typically pedal less hard when descending, so UFT chain energy consumption is primarily a concern while climbing. Climbing speeds, and hence bump forces, are low, limiting bump induced suspension movement.
The commercial success of many different kinds of UFTs suggests efficiency differences between frames are small and energy lost to chain growth is smaller than the amount of additional energy lost to bumps in a hardtail or URT. The situation is similar with braking. When analyzing how a rear suspension responds to braking, there are only two kinds of swingarms. Those which attach to the front triangle with one pivot and those which attach to the front triangle with two pivots. URTs and monopivot UFTs comprise the former category. Faux bars, Horst links, VPPs, and FBBs comprise the second category. A trivial control volume analysis of the rear wheel and swingarm of a monopivot shows braking exerts the compressive torque on the swingarm
ts = -fgrg
where fg is the force the tire exerts on the ground and rg is the position of the ground relative to the pivot. When the swingarm is attached with two pivots the torque induced by braking becomes
ts = -fg - rg' + fup - rup + flp - rlp
where fup and flp are the forces at the upper and lower pivots and rg', rup, and rlp are the forces' positions with respect to the swingarm's effective pivot location. Where -fg - rg' is always compressive, linkages can be designed such that the rest of the right hand side is compressive, extensive, or zero. While there's strong consensus extensive torque is a bad thing, since it exacerbates fork dive by inducing brake jack in the rear suspension (within the swingarm's mechanical limits; the amount of jack cannot exceed the amount of sag), there's no consensus around compressive torques. Some riders feel the zero case, where rear braking forces don't cause the swingarm to move, is a very important aspect of suspension design. Others don't care. Many designs are marketed as fully active, brake independent, or as eliminating brake forces (it has, however, been my experience stopping bikes where the brakes don't exert any force is difficult) . Without access to Linkage Professional it's non-trivial to make an independent assessment of these claims, as writing a linkage solver to obtain the pivot forces takes some time. Sasaki makes conflicting statements in this area, but either claims there's little or no difference in the behavior of linkage bikes and monopivots under braking or that there's no difference at all. Independent rider observation indicates the differences are at most small and, personally, I suspect a mathematical proof exists to show ts is a function only of the effective pivot location.
It's unclear what it means for a suspension to be fully active under braking. To get a sense of the design space, consider a worst case monopivot where the pivot is as high as possible. That would be a top tube pivot, which on the Klein Mantra is about 70 cm above the ground. The maximum deceleration a rear wheel can provide before locking up is maybe 0.5 m/s2. Assuming a combined bike and rider mass of 75 kg, the braking force is about 40 N (due to the wheels' moments of inertia), so -fgrg ≈ -28 Nm. The shock has about a 16.5 cm moment arm, so an additional 1.7 kN is needed to counter the torque. A näive analysis using the sag figures from the torque residual analysis above would expect the shock to provide this force, and therefore anticipate about 20 mm of compression. However, braking causes weight to transfer from the rear wheel to the front wheel. Neglecting the mass of the front triangle and fork, the resulting extensive torque on the swingarm is approximately
tr = mrarr
where mr is the rider's mass, a is the acceleration from braking, and rr is the height of the rider's centroid above the swingarm. With a 60 kg rider, tr ≈ 24 Nm, leaving a net compressive torque of -4 or -5 Nm, which translates into 3 or 4 mm of compression and about a 20% increase in the shock's loading. This additional preload will result in a 20% increase in bump forces. The suspension is therefore less active, but not significantly so. If only rear braking forces are considered, it would therefore seem desirable to design the swingarm such that ts + tr = 0, which isn't too hard to do since the degree of cancellation between these two terms is independent of how hard the braking is, as both are proportional to acceleration. The point where optimal rear brake torque cancellation on a monopivot occurs is about halfway between the Mantra's top tube pivot and the usual UFT monopivot placement. (This location correlates well with the pivot placement of sweet spot URTs, suggesting Castellano's motivation for using the phrase sweet spot comes from the pivot location mostly canceling both brake and pedaling forces.) A typical UFT monopivot is roughly the opposite of the Mantra, showing a net extensive torque of ts + tr ≈ 3.5 Nm in the situation described above, causing some brake jack but also making the suspension more active by reducing the preload on the shock.
So, arguably, a fully active swingarm should be one which implements ts + tr = 0, not ts = 0. The problem with this approach is bikes have front brakes, the use of which will contribute increase tr but not ts. From a broad design standpoint, it's therefore preferable to have the suspension exhibit net compressive torque when only the rear brake is used in order to partially compensate for brake jack induced by use of the front brake. But not so much as to cause a great deal of squat when the front brake is not used. However, utilizing ts for this purpose requires the rear shock compress, which in turn means the pedal platform must be broken so that the shock is active; pedaling forces vary faster than braking forces, so if the shock's locked against pedaling it's unlikely to respond to braking either. Conversely, a locked shock is equivalent to ts + tr = 0 which, incidentally, is a hardtail.
| Conclusions |
As discussed above, what it means for a swingarm to be fully active is debatable and, further, achieving full activity is not necessarily desirable. The limited pivot placement of UFTs has led riders to prefer pedal platform shocks, whose purpose is to create a suspension which is explicitly not fully active. However, the idea behind the hype is quite simple; some suspension design is optimal. As the sections above show, the pivot location of sweet spot URTs is more or less optimum respect to pedaling, braking, and bump absorption. But URTs' behavior with out of saddle riders is such a big problem virtually every full suspension rider has switched to UFTs with lower pivot locations. The engineering design problem for mountain bike rear suspension is therefore clear; how does one build a sweet spot UFT? Chain growth is the only thing which makes a sweet spot UFT infeasible. That problem is easily solved by routing the chain from the bottom bracket to the pivot and then adding a second chain running from the pivot to the rear axle, but the resulting zero chain growth comes at the expense of weight, complexity, and reduced power transfer efficiency. While internal transmissions may eventually provide an alternative solution, their current high cost, lower efficiency, and greater weight relative to a conventional drivetrain limits their appeal. UFT frame designers and riders therefore make tradeoffs between chain growth and pivot position. Pivots near the bottom bracket minimize chain growth and therefore tend to result in the most active suspensions. Such pivots compromise on pedal bob and bump response, though these limitations can be mitigated with platform shocks and linkages which require little force to compress. Most bikes in this category are faux bars and this form of suspension is common in cross country and all mountain frames. Pivots forward of the bottom bracket offer the best large bump response but the greater anti-squat reduces suspension activity when the rider is pedaling. Such bikes are usually implemented as monopivots, though some VPPs qualify as well. The majority of downhill and freeride frames are monopivots. Pivots behind the bottom bracket usually offer more anti-squat and better small bump absorption, but have worse large bump response and may have large amounts of chain growth. Examples are Horst links and Giant's Maestro line, both implemented using linkages. Well designed FBBs or URTs sacrifice as little suspension activity as possible in exchange for a pivot location outside of the UFT design space, but such frames typically have only niche appeal.
| What I Think About Suspensions |
My local trails are relatively smooth and range from hardpack to soft over hard depending on the season. There are some rock gardens, but the majority of trail miles have generally infrequent rocks and roots. Nearly all of the riding is seated; steep, technical, out of saddle ascents and descents are rare, though there are plenty of places where you can run out a couple miles of continuous granny ring climbing. Full suspension is nice, but maybe half the bikes on the local trails are hardtails and the occasional rigid turns up. I switched from a rigid to a year end closeout Specialized Stumpjumper S-Works hardtail in late 1996. The Stumphumper, as I've come to call it, was a total lemon and Specialized failed to honor the warranty (the list starts with badly butted rims, rimstrips which cut through in about a week, an incompletely pressed headset, and gets steadily worse until it finishes with wheels so poorly built the rear tacoed on its own accord, which Specialized refused to warranty because I'd trued it into rideable shape to get home). Unsurprisingly, I switched to a Klein Mantra Race in 1997, upgraded to a 65 mm travel Marzocchi z.2 Bomber and Race Face Turbine LP cranks, and rode it for eleven years. Wore out the rims, hubs, and rear shock and went through two cassettes and sets of chainrings, along with a lot of chains, brake pads, and tires in 15,000 miles or so miles. It was eventually stolen (use a U or chain lock; cable locks are no good no matter how beefy) and the majority of my trail miles are now on a 2005 Jamis Dakar XC Pro I picked up used from Kylie Krauss. The bling on the Pro is overkill, but I appreciate the longer front travel and distinctly more active suspension.
I'm partial to high quality shocks but am not terribly fussy about other components. I'm not a heavy guy and, as an XC rider who likes keeping both wheels on the ground, don't ride a bike nearly as hard as some. So I prefer the lower bump forces and greater efficiency which come from a suspension which compresses easily. I also like bars at least an inch lower than the seat, which some bikes lend themselves to and some do not, really steep head tube angles, and frames with high lateral stiffness. The head angle and force needed to compress the suspension are the two best predictors of how much I'll like a bike. As of 2007, the XC full suspension frames with 71° or steeper head angles were the Giant Anthem, Ibex Asta, Jamis Dakar, Rocky Mountain Element, Santa Cruz Blur XC and Juliana/Superlight, Specialized Epic, along with a few expensive framesets from boutique manufacturers (and by expensive I mean "costs more than a NOS bike with a full XTR group"). The two high compression force designs in this group are the Epic and the Anthem; the rest are all low force. I didn't like the Epic at all—I prefer washer based platforms to the inertial valve on Fox's TerraLogic and Brains—though I liked the Anthem's race oriented rider position and 72° head angle enough to be tempted. Santa Cruz shaves too much weight off their frames to produce a bike which is as responsive as I'd like, even after the 2007 rear triangle upgrade on the Juliana/Superlight. I found the Blur to be so sluggish I'd rather ride the all mountain, 68.5° head angle Jamis XLT, which feels more agile to me. I had problems with big hits popping the chain off the Blur's middle ring too. In comparison, both the Element and Dakar are pleasingly responsive. Rocky and Jamis's frames have virtually identical geometry, but I'd give the edge to the Dakar linkage's slightly lower compression force. I couldn't find an Ibex Asta to try. While Ibex's faux bar linkage is quite similar to the Dakar linkage, the Asta geometry's a bit slower than the Dakar, so I suspect I personally wouldn't like it quite as much.
Overall, my sense is low chain growth designs, be they faux bars or Horst links, with platform shocks are the current best option for XC riding. Higher chain growth designs, like high pivot UFTs and most VPP frames, I've ridden seem slightly less efficient and slightly less active at a comparable amount of platform. When I was looking for a bike in 1997 my second choice was a Specialized FSR for essentially this reason. I ended up with the Mantra because, at the time, the only way to control bob was to build platform into the frame by raising the pivot, though the Mantra's 71.5° head angle didn't hurt either. Even though the suspension design's completely different and has 60% as much travel as the Mantra the Dakar is, to me, a logical successor since it's the bike I would have liked to buy in 1997.
| back to top |
copyright 1997–2009 by Todd West
last modified 2009.08.20