Geodesics on a Cone
Exploring a singular surface
During a mathematical physics course, a professor asked what appeared to be a simple question about geodesics on the cone. After thinking the problem over for a weekend, I came up with an answer that agreed with hers -- and we were both wrong. I’ve spent another week pondering the problem, and think I finally have a solution.
Geodesics
When mathematical physicists talk about geodesics, they don’t have the layman’s definition "the shortest line between two points" in mind. While pithy, this definition is misleading in two ways: (1) the line is guaranteed to be shortest only in a Euclidean space (e.g., a plane), and (2) there may be more than one geodesic between two points.
Consider two nearby points on a sphere. There’s an obvious shortest path between them. Yet there’s another path that fits the mathematical definition of a geodesic, and that’s the rest of the great circle containing the points. Each of these is a straight line on the sphere’s surface.
![[two points on a great circle of a sphere]](sphere.two.geodesics.png)
Now consider the poles of a sphere. No matter which direction you leave the north pole, if you travel in a straight line you’ll always end up at the south pole. For antipodean points on a sphere, there are an infinite number of geodesics.
![[multiple meridians between poles of a sphere]](sphere.meridian.geodesics.png)
So a geodesic isn’t necessarily the shortest line between points, nor need it be unique. Rather it’s a straightest line between two points.
With that in mind, we can tackle the question the professor had posed: how many geodesics can there be between two points on a cone?
Geodesics on Cones
We could try to solve this analytically, but in general equations for geodesics are messy and chock full of partial derivatives. Let’s put that approach aside and consider the problem geometrically, generalizing an answer from different cases.
The simplest case is the cone of zero height, which is the plane. Its geodesics are those of the plane: straight lines. So for the zero-height case there is exactly one geodesic between any two points.
Adding a little height to the cone changes the situation dramatically. To simplify the analysis, we use a fact I won’t prove here: if we cut the cone along a meridian and unroll it, the geodesics on the cone become straight lines in the plane. This means we can analyze cones solely with two-dimensional diagrams (which are much easier to draw).
Let’s look at a cone of little height, cut and unrolled:
![[circle with a small sector removed]](unrolled.cone.gif)
We’ll simplify our analysis by looking only at those geodesics that terminate at a given point. We can do this without losing any generality because the cone is radially symmetric and scalable. So let’s put our fixed point (F) at the outer end of the meridian we cut along:
![[circle with a small sector removed and black dots at end of cut meridian]](two.images.of.F.gif)
We denote F by a black dot. There are two images of F, not one, but they’re the same point because the two straight lines are the same meridian.
Without loss of generality, we can assume that the other varying endpoint V is no further from the apex than F. (Otherwise, just swap F and V.) We’ll denote V by an open dot.
Now that we’ve got our notation set, let’s look at the cases for the almost-flat disc.
![[one geodesic from F to a point nearby]](almost.complete.1.geodesic.gif)
Here’s a case where there’s one geodesic between the two points. You might think to draw a straight line between V and the other image of F, but that’s not allowed; lines can’t cross the gap.
There’s another case to consider: what if V is on the opposite side of the cone from F? When you travel from one side of the cone to the other the apex must be on either your right or your left, so it would seem that there are two ways to get there. Is this correct?
![[two geodesics from F to a point opposite the missing sector]](almost.complete.2.geodesics.gif)
It is, as the illustration shows. So depending on where V is, there can be either one or two geodesics. The key to finding the dividing lines between the 1-geodesic and 2-geodesic regions is to realize that a straight line from an image of F must stay completely within the unrolled cone. This restricts the 2-geodesic region to the area reachable from both images of F. In the following images, the gray regions indicate which portion of the cone can be reached from a particular image of V.
![[on left: half-disk containing one image of the cut meridian; on right: half-disk containing other image of the cut meridian]](almost.complete.hemidisks.gif)
Everything outside the intersection of the two hemidisks is a 1-geodesic region. Note that the 1-geodesic region really is one region, as the two regions below are joined along the cut meridian.
![[circle with small sector removed, divided into large 1-geodesic region and small 2-geodesic region]](almost.complete.regions.gif)
As the cone gets steeper, the 1-geodesic region shrinks and the 2-geodesic region grows.
![[two-geodesic region dominates 1-geodesic region]](2-region.grows.gif)
When the central angle θ decreases to π, the unrolled cone becomes a hemidisk. The 1-geodesic region degenerates into the meridian containing F, and the rest of the cone is a 2-geodesic region.
![[point in interior of half-disk has 2 geodesics from F]](hemidisk.2-region.gif)
![[point on meridian containing F has 1 geodesic]](hemidisk.meridian.gif)
When I first analyzed the problem, my solution (and the professor’s) extended little further than this. Yet it teased at my mind, and when I first tried to write about it, I realized this analysis was incomplete. Let’s extend it.
As θ decreases still further, the central angle becomes acute. The 2-geodesic region still exists, like before.
![[point in interior of convex sector has 2 geodesics]](convex.2-geodesic.gif)
However, something new has occurred: straight lines can cross the cut meridian and still stay within the figure, leading to the creation of a new 3-geodesic region. You can picture this as traveling all the way around the cone and returning to the cut meridian.
To find a V such that there are three geodesics, rotate a copy of the unrolled cone around the apex until the cut meridians are congruent. Points that have three geodesics will be those whose images in the rotated copy can be connected to F by a straight line entirely within both copies. The longer geodesic in the first figure below demonstrates this.
![[two images of V are reachable from left image of F, one in sector, one in rotated image of sector]](convex.image.1.gif)
![[an additional image of V in a rotated sector is reachable from right image of F]](convex.image.2.gif)
Each red line is a different geodesic, leading to a total of three for this particular V. (Any other lines we could draw between images of F and V can be carried to one of these geodesics by a rotation.)
![[flat cone with three geodesics in different sectors]](flat.cone.with.three.geodesics.png)
Unrolled cone with three geodesics
![[perspective image of cone with three geodesics, one of which self-intersects]](cone.with.three.geodesics.png)
Corresponding geodesics on the cone
As θ continues to decrease, the 3-geodesic region grows and the 2-geodesic region shrinks. This continues until we reach the next transition point: 2π/3. At this angle, three images of the cone fit into the disc, and the 2-geodesic region degenerates to a line. Unlike the case when θ is π, however, the 2-geodesic line isn’t the meridian containing F -- it’s the line bisecting the 3-geodesic region (which means it’s on the opposite side of the cone). In the diagrams, the 2-geodesic region is a dashed orange line.
![[three images of V in interior of sector are reachable from F]](third.3-geodesic.gif)
![[V on bisector of sector is reachable from only two images of F]](third.2-geodesic.gif)
By now you should be able to guess the pattern. As θ decreases below 2π/3, a 4-geodesic region appears and grows while the 3-geodesic region shrinks. As when θ decreases below 2π, the 4-geodesic region appears directly opposite the meridian containing F and expands toward it.
When θ decreases below 2π/5, the 3-geodesic region disappears and a 5-geodesic region appears. Likewise, when θ decreases below 2π/6, the 4-geodesic region disappears and a 6-geodesic region appears, and so on. Eventually you’ll be drawing diagrams like these:
![[five images of V are reachable from F]](5-geodesics.gif)
Five geodesics
![[six images of V are reachable from F]](6-geodesics.gif)
Six geodesics
Trust me, you don’t want to have do this. A general solution to the problem is much better.
The General Solution
Whenever θ decreases beneath 2π/n, an (n-2)-geodesic region disappears and an n-geodesic region appears on the same side of the cone. When n is even the new region appears on the same side of the cone as F, and when n is odd the new region appears on the opposite side of the cone.
So there can be any number of geodesics between two points on a cone, provided you choose θ appropriately. There is always an n-geodesic region and an (n-1)-geodesic region (except for the flat cone, which has no (n-1)-geodesic region).
There was more to this problem than any of us expected.
Craft Corner
Here are some models of cones that you can print and assemble. They’re designed for a color printer, but are fine B&W.
These models have example geodesics already plotted.
- Cone with 1 & 2 geodesics: PDF [2K], EPS [158K]
- Cone with 2 & 3 geodesics: PDF [2K], EPS [160K]
- Cone with 3 & 4 geodesics: PDF [2K], EPS [171K]
- Cone with 6 geodesics: PDF [2K], EPS [168K]
To demonstrate that these really are straightest lines, make a small hole through the paper in the center of each white circle. After assembly, stretch a thread from a hole to the black circle and pull taut. It will lie along one of the marked geodesics.
Do-it-yourself versions of above: no geodesics are plotted, but the boundary between regions is shown so that you can choose your own example point(s) in each region.
- Cone with 1- & 2-geodesic regions: PDF [2K], EPS [151K]
- Cone with 2- & 3-geodesic regions: PDF [2K], EPS [149K]
- Cone with 3- & 4-geodesic regions: PDF [2K], EPS [150K]
(A DIY version of the six-geodesic model isn’t interesting because in the original model θ is 2π/6 and the 5-region is degenerate.)
Cones and Cylinders
Why does the number of geodesics increase without bound as θ approaches zero? In retrospect, the answer is obvious: the closer θ comes to zero, the more the cone locally approximates a cylinder. Between any two points on a cylinder not on the same parallel there are an infinite number of geodesics: on a cylinder geodesics are helices, and varying the tightness of a helix’s coils changes how many times it goes around the cylinder before it reaches the endpoint. There’s no upper bound; you can make it as tight as you prefer.
As the cone locally looks more like a cylinder, geodesics can wind around it more and more. In that sense, the cylinder is the limit case of a cone of increasing height.
![[six colored, self-intersecting geodesics in one sector]](6-geodesic.color.gif)
Why Do Cones Have Zero Gaussian Curvature?
A cone is a surface of revolution. In the diagram below, the red line is a meridian, and the blue circle is a parallel.
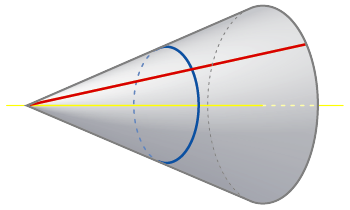
The Gaussian curvature at a point is the product of the principal curvatures at that point. On a surface of revolution, the principal curvatures are measured along parallels and meridians. The meridians of a cone are straight lines, with zero curvature, so at every point on a cone the Gaussian curvature is zero. Because cones have zero curvature everywhere, we can unroll them and analyze their geodesics on the equivalent flat surface.
Last updated 27 October 2007
http://www.rdrop.com/~half/Creations/Puzzles/cone.geodesics/index.html
All contents ©2004 Mark L. Irons